tl;dr: we argue that the “free option” problem is potentially substantial in the current specification of EIP-7732: Enshrined Proposer-Builder Separation
joint work with @0xSybil and @BrunoMr
Special thanks to @dataalways for extensive discussions and to Fei Wu and @sui414 for shared data. Here is Part II.
Imagine you are at the roulette table in a casino and somebody makes you an offer: you get the option to revert the next spin of the roulette wheel if you don’t like the outcome. Reverting here means that all placed bets are ignored and every gambler has the same amount of chips as before the spin of the wheel. How much would you be willing to pay for that option? How much would you bet? And how likely is it that you will exercise the option?
You should value it a lot. You get an expected return of almost 50% with zero downside risk. You would like to bet as much as the bank allows you to bet if you had the option. And you would exercise the option every time you lose, i.e. a bit more than half of the cases.
The “free option” problem is the following: a builder that commits to an execution payload and wins the block auction, can wait to invalidate the execution payload until shortly before the payload timeliness committee (PTC) deadline (for the details see below). In case new information arrives after the commitment but before the PTC deadline and that information makes it preferable to publish an empty block rather than publishing the block committed to, the builder can choose to do so.
We argue that the current specifications of EIP-7732 (8s to exercise the option) could make it a valuable option to builders and a large fraction of blocks could end up empty, with more empty blocks in times of high volatility and around important events. We moreover, argue that the problem becomes much more severe in a potential future where more and more liquidity and financial activity moves to Ethereum.
Casinos, Binance and Ethereum
We can quite easily modify the above casino story to see the intuition:
Imagine you are trading BTC or ETH (spot and futures) in a highly liquid market such as Binance and someone offers you the option to revert all of your trades after 8 seconds if you don’t like how the market has moved within these 8 second. How much would you be willing to pay for that option? And how likely is it that you will exercise it?
Again, you get a positive expected return with zero downside risk. Liquidity determines the size of your position and how much value you can extract: at current market conditions (as of writing this) you can trade ~10 BTC on the smallest tick (1 cent for the spot resp. 10 cents for futures which means less than a dollar of slippage cost). Let’s ignore Binance fees for the moment (not because they aren’t substantial, but because we want to figure out what would happen if the same amount of liquidity would be traded on chain where hopefully there are no rent seeking middle men). So the casino allows you to bet around a million $ per spin. The average value of a spin now is ~1-3 bps (see below) instead of close to 50%. Thus, we are at 100-300$ option value on average per spin. On the other hand, Binance is a casino with several (correlated) roulette wheels: major token pairs have significant liquidity (although less than BTC) which should give us a factor 3-5 in comparison to only trading BTC. 300-1500$ for 8s, not bad. If you only trade BTC, you should exercise the option about half of the time (over 8 seconds it’s almost a coin toss whether BTC goes up or down). If you trade other things as well, then you get less exercises of the option (diversification reduces risk), but still significant chances of exercise.
Ethereum block building is of course different:
Simplifying, but not oversimplifying too much, if you are an (integrated) builder, your value for the block 8 second after having committed to it is a positive constant term (whatever block value you have at commitment from “non-arbitrage” MEV) + a random term (you directional risk if you take on a position e.g. in ETH by trading on chain). Exercising the option in case of a bad realization of the random term will also make you lose the positive constant value. But as in the casino example and the BTC example you can amplify the random component as much as (on-chain) liquidity allows you to, thereby increasing the overall return. Thus, you might exercise the option less than half of the time, but more often than we like, provided there is enough liquidity on chain.
Put differently, having the option to invalidate the block after eight seconds changes the kind of blocks that builders will build and the option will exercised much more often than naive extrapolation from current data would suggest.
Some napkin math & preliminary conclusions
Suppose ETH returns (log prices) are normal (over short short time intervals they really really aren’t, but it’s an approximation good enough for napkin math standards and ceteris paribus everything would be much worse with fat tailed returns). A napkin math approximation of the option value with 0 mean is
where L is notional of my position and \sigma_\tau is the volatility over \tau seconds. In other words, and most relevant for ePBS design considerations:
The value of the option is increasing in volatility and increasing in liquidity. As volatility (and also liquidity to some degree) is increasing in time, its value is increasing in the time to expiration.
We can get a more sophisticated version of napkin math if we look at the positive constant term as well. Let’s call it \mu for MEV. If we factor it in we get the absolute value of a normal with positive mean as the option value. Thus, the value of the option per unit of MEV is
and we get a corresponding probability of option exercise of \Phi(-\frac{\mu}{\sigma_\tau L}) where \Phi is the cumulative distribution of a standard normal. Thus, whether or not we have a problem depends on the ratio \rho:=\tfrac{\mu}{\sigma_{\tau}L}.
In other words, the napkin math tells us that everything else being equal, the free option problem gets worse if we reduce (non-arbitrage) MEV per unit of liquidity on-chain. As reducing on-chain MEV is a goal that many solutions and applications work towards (e.g. through better AMM design, middle-layer infrastructure, encrypted mempools and so on and so forth), paradoxically, the free option problem gets exacerbated the better we make the on-chain trading experience.
Next let’s go to the ultimate piece of napkin math: suppose you are an arbitrageur who wants to make use of the CEX-DEX price discrepancy at the end of the slot. One (suboptimal) way of doing this as an integrated searcher-builder would be, at the beginning of the slot, to place a top-of-block DEX swap in a block and cancel the block bid close to the end of the slot if the price moves against you on the CEX in the meantime. If it moves in your favor you would hedge on the CEX. This gives you half of the value of an optimally executed arbitrage trade at the end of the slot, as you are only trading in one direction and prices go up and down with equal likelihood. In other words:
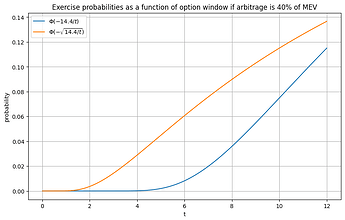
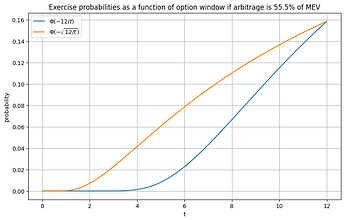
The free option should get you about half the pure CEX-DEX arbitrage gains you could make in a world with \tau seconds length slots. If CEX-DEX arbitrage accounts for x% of block value, then \rho=\frac{\mu_{12sec}}{0.5/0.4\tfrac{x\%}{1-x\%}\mu_\tau}=\frac{4(1-x\%)}{5x\%}\frac{\mu_{12sec}}{\mu_\tau} where \mu_{\tau} is the MEV we could capture per block if slot times were \tau seconds.
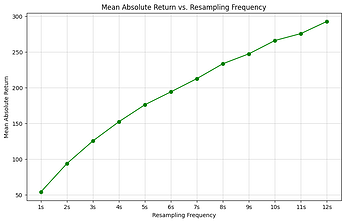
How arbitrage gains scale with slot time is a contested question. But the factor should be between \sqrt{\tfrac{12s}{\tau}}\leq \rho<\tfrac{12s}{\tau}, i.e. for \tau=8s, we have 1.2247<\rho<1.5 . This is because volatility scales with the sqrt of time in theory (assuming a Gaussian process) and practically, in short time intervals, between the sqrt and linearly in time. Thus, the probability of executing the option in case of 55.5% arbitrage MEV is between \Phi(-1.5)=6.68\% and \Phi(-1.2247)=11\%. The following graph, illustrates hypothetical exercise probabilities with sqrt resp. linear scaling of MEV in time. While the estimates might be quantitatively off, qualitatively we should expect this behavior. The longer the free option window relative to the slot time, the worse the problem.
There are a bunch of immediate questions that are best answered empirically (as we partially do below):
- How does volatility and therefore value scale with \tau?
- When is \tau too long?
- What is the expected cost of exercising the option \mu as a function of liquidity and slot time?
Time to expiration in ePBS
In current specs of ePBS [1,2,3], the validator-builder handshake starts with a commitment at t=0s, the builder signs an ExecutionPayloadHeader and the bid is directly removed from the builder’s beacon chain balance and credit to the beacon block proposer, but the delivery of the blocks and blobs now passes two checkpoints enforced by the 512-member Payload-Timeliness Committe (PTC). At t=4s there is the payload deadline, if not enough PTC votes attest that the full execution payload has been propagated, the slot is flagged empty and there wont be any state transition. At t=10s, a second PTC pass requires the blobs are available. In case sufficient PTC votes, the slot is re-labelled as empty, and the Payload is in-validated. Since the builder has already paid in the moment of taking the decision to release or not release the blobs, the decision remains in the builder’s hands, and so, the builder enjoys a time-bounded free-option of approximatly 8s (assuming that 2s are needed to safely propagate blocks among PTC members).
Figure 1. Dual-deadline PTC vote in ePBS (Adapted from Dual-deadline PTC vote). The diagram shows that the payload must be available early in the slot (≈ 4 s) to give clients time to execute it, whereas blobs enjoy a longer propagation window until ≈ 10 s. Red vertical markers highlight the last moment when a strategic builder can safely release the payload, and later the blobs, to almost guarantee inclusion.
Some empirics
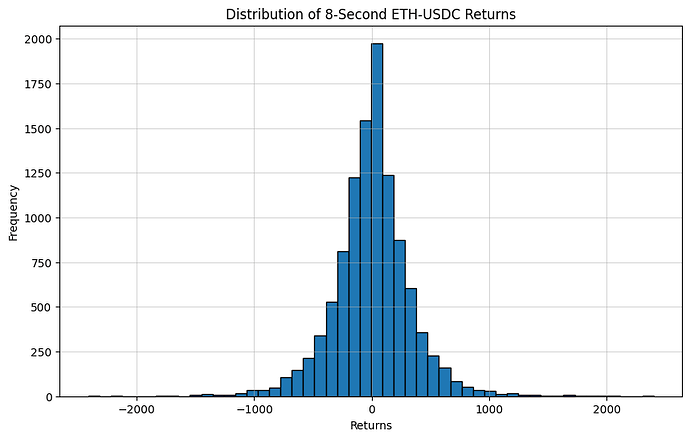
Let’s look at the actual performance. Here is a histogram of returns for one million notational traded every 8sec in ETH-USDC based on the last trading day (21 July 2025):
We choose, one million notational because that is about the size of liquidity we can access on Binance for ETH-USDC/T pairs (with close to no slippage cost). We get a realized average value of the option of ~117$ (~1.26 Million $ per day). Whether you choose to always go long or always go short (or randomize) does not really matter for the realized average value and also does not for the realized frequency of exercising the option (around 48.6%). Of course a sophisticated trader might be able to extract more value, e.g. if she has a signal that allows her to choose with better than 50% the direction of the price over the next 8 seconds. The point is that even an unsophisticated trader makes a lot of money.
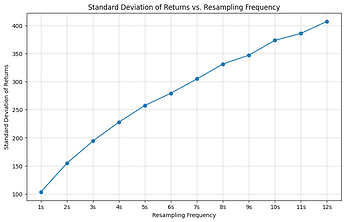
Let’s also look at how arbitrage gains scale with time. We can observe at least two things: first that the napkin math model that arbitrage gains are proportional to volatility and that volatility is proportional to the sqrt of time is not too much off. Second that the option value and therefore, arguably, the free option problem is substantial for modestly long time to expiration.
Caveats and Qualifications
We want to caveat that the “free option” might not be used by builders even if highly profitable, as there might be social slashing and reputation effects at play. If validators blocklist builders who have missed payload delivery, this can make exercising the option for short term profit not attractive. Similarly, if order flow providers, searchers and other transaction originators, avoid builders who have failed payload delivery repeatedly in the past, builders might refrain from using the option. While we hope that these “good” equilibria would play out in reality, it is important to note that there are also other equilibria where social slashing does not happen and reputation effects are not strong enough to enforce “good” builder behavior. Protocol design should arguably not rely on good equilibria being played, but should provide robust incentives in a variety of scenarios. Hence, we think that the analysis of whether the option is valuable to exercise absent of repeated games effects is important.
Second, the free option problem is a problem if we want to use L1 as execution layer in the future. If the L1 is primarily used for data availability and settlement and we primarily use it to post blobs or settlement transaction, the free option problem becomes less important.
Conclusion
Whether the option value of not releasing a block matters depends on several factors: volatility, liquidity, spreads, on-chain MEV, and the expiration time of the option. Yet as long as Ethereum supports real economic activity, the ePBS free option will keep a non‑negligible value with the current parametrization, and builders have an incentive to exercise it while entry to the ePBS market stays permissionless. Each time they do, users suffer: their trades remain pending and trading venues widen spreads. The number of empty blocks can vary, but the moments when, arguably, users most need to trade, namely periods of high volatility, are exactly when empty blocks spike. Honest builders who always release payloads and blobs on time then can become less competitive. That dynamic can trigger a vicious spiral in which validators stop block‑listing the withholding builders to earn higher fees, until almost every builder adopts the same strategy.
We see three groups of economic mitigations in the current ePBS design: block‑listing, shortening the option window, and making the option effectively more costly. Block‑listing builders that fail to release the payload or the blobs on time can work for a while, but it is fragile. Any validator can disable the list with a simple configuration change and is tempted to do so, because allowing the full set of builders to bid, including those that exercise the option, boosts competition and therefore expected auction revenue; once one staking pool unblocks them, the rest will potentially follow.
Shortening the release window for blobs and payloads, reduces the option’s value quickly. Cutting the free option window from eight seconds to six, or even better three seconds would sharply lower the probability that builders exercise the option. One must, however, balance this against the fact that windows that are too short can increase the risk of re‑orgs.
Finally, exercising the “free option” can be made more costly. In today’s ePBS spec, releasing or not releasing costs the builder exactly the same: the bid paid in the ePBS auction. Not releasing is therefore a sunk cost. Introducing a penalty for failing to release either the payload or the blob (possibly with different penalties, because blobs give the builder more late‑MEV value than payloads) can strongly disincentivize the strategy. For any fixed cost there will exist rare events where deviation is still profitable; the goal is not to eliminate the strategy in every edge case but to make it unprofitable in almost all practical situations, thereby leaving only negligible negative externalities while preserving ePBS’s scalability benefits. The penalty could be static, for example one ETH per unreleased block, or dynamic, similar to EIP‑1559 but keyed to the share of unreleased payloads, blobs and previous MEV bids. The fee must be large enough to make the option essentially worthless for 99.9 percent of the time, yet small enough to keep entry barriers low and MEV bids competitive.
In short, today’s ePBS design may solve scaling, but it can also distort the block‑building market and hurt users. Tightening PTC deadlines and/or slashing builders on non‑release, look like the most promising fixes if we want to implement ePBS.
Yes, this, seems to be a fundamental problem with any design that has full “pipelining”, modulo some other clever solutions or re-thinking what we do with blobs in general. So I don’t have the answers, but I acknowledge the problem.
But we would need to look at the quantiles to know how often it would be exercised. But without knowing that in detail, I would believe you that we currently don’t have the liquidity on chain to make this option as useful as it would be in other regimes. But also averages on the volatility don’t give you the full picture. By chance we picked a higher vola day for our very preliminary data analysis. But hopefully, we don’t only want to produce >99% non-empty blocks on average per year, but >99% on average per day.