tl;dr: We test the theoretical predictions we made in Part I empirically, by looking at block level data in Ethereum and check whether the option would have been profitable to exercise on realized blocks (as opposed to optimally built blocks if builders had factored in the availability of a free option). In realized blocks, option value (3.67 ETH per day) and average exercise probability (0.82% per block) is low on average, but high (>40ETH and >3.5%) on high volatility days.
Joint work with Fei Wu, @0xSybil , @boz1, @BrunoMr
Thank you to @dataalways, @Quintus, @soispoke, @sui414 for comments on a first draft and data.
In our previous post, we made several theoretical predictions about the free option problem. Most importantly
- The value of the option is increasing in volatility and liquidity.
- The longer the free option window relative to the slot time, the worse the problem.
- Additional penalties in case of failing PTC deadlines would be a solution to the free option problem (while potentially introducing other problems).
- The larger the share of non-statistical MEV in the block, the less of a free option problem we have.
In this part, we want to test the theory and, arguably more importantly, quantify the size of the problem. We use a sample of realized blocks in Ethereum from January 2024 to March 2025 and a data set of bundles that have been identified to be associated with CEX-DEX-searchers, together with corresponding marks of bundles based on CEX prices at different mark-out times to estimate whether the option would have been profitable to exercise on these blocks and trades.
There are obvious possible shortcomings of our methodology on which we comment more in the penultimate section. Arguably, the most important one is that we possibly underestimate the effect because we restrict ourselves to blocks built without the free option available. Searchers might size their positions differently if they had a free option. Other strategies than reverting arbitrage trades can be carried out with a free option. In short, block builders that use the free option will build different blocks, potentially increasing the value of the option and the probability of exercising it.
With these caveats, the analysis should be read as an attempt to get a first estimate on the quantities of interest, not a definitive answer to all questions.
Sample description
Our dataset covers every Ethereum block between 1 January 2024 and 7 March 2025. Using the approach of Fei et al. 2025 for identifying CEX-DEX arbitrage searchers, we analyze trades originating from addresses associated to 23 CEX-DEX searchers (wintermute, SCP, Galio,…). For each trade, we record the amount paid to the block builder (the priority fee plus any direct block.coinbase transfer) and the searchers’ resulting balance changes. We also collected Binance mid price data for the traded pairs, 0,1,…,8 seconds after the slot time. i.e. until the last moment at which the block builder could still exercise the ePBS’s free option by not delivering the blobs. As in the paper, we restrict our attention to trades with tokens that are listed on Binance, so the final sample consists only of blocks containing a CEX-DEX arbitrage opportunity in those tokens; these blocks represent 56% of the total number of blocks.
Methodology description
For each block with a trade covered by our data set, we compute the total block value (TBV) v in ETH that is, the total amount of priority fee and block.coinbase payment collected by the block builder. We calculate the sum of transfers p in ETH by CEX-DEX searchers to the builder and deduct it from the TBV.[1] We then calculate the market value of the CEX-DEX searcher bundles at time t=8s (and at intermediate times to check the effect of shortening the option time window), i.e. if the searcher trades x amount of token A for y amount of token B on a DEX, then we calculate \pi_8=p_8^By-p^A_8x where p_8^A,p_8^B are the Binance mid prices of the tokens A and B converted to ETH. We then calculate v-p+\pi_8 to obtain the block value after 8 seconds. [2] The option is profitable to exercise if the block value at time t=8s is negative, i.e. v-p+\pi_8<0, and the realized value of the option is the value made by the builder when having the option minus the value he makes without having the option, i.e. \max\{0,v-p+\pi_8\}- (v-p+\pi_8).
Option Value and Exercise Probability
In realized blocks from our sample we make the following observations, largely in line with the theory we proposed. First let’s look at the frequency of the option being profitable to exercise. We observe low averages but high variability in the data. More precisely
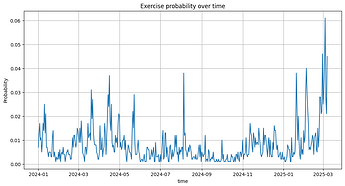
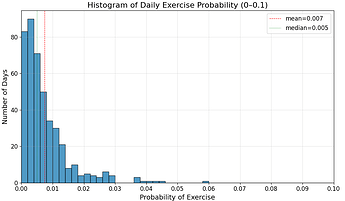
- The probability of the option being profitable to exercise is low on average for 8 seconds option time window: in 0.82% of the observed blocks, it is profitable to exercise the option.
- There is high variability over time: days of higher frequency of 3.5% or larger of profitable exercise appear occasionally.
Next, let’s look at the realized option value which is the value of the option for the built blocks. We find the following:
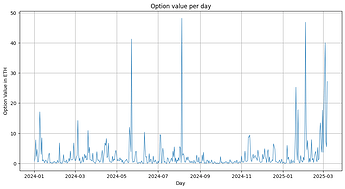
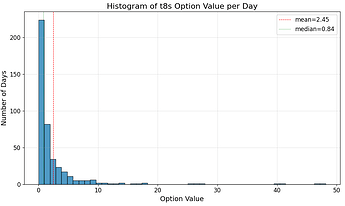
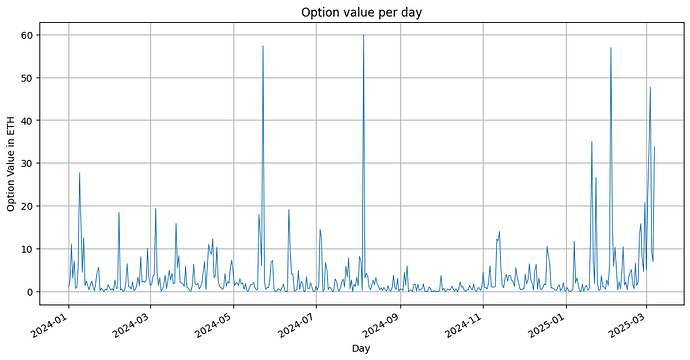
- The realized option value is low on average (~3.67 ETH per day).
- There is high variability over time.
- Option value is very asymmetric. A few trading days in our sample contribute to most of the option value.
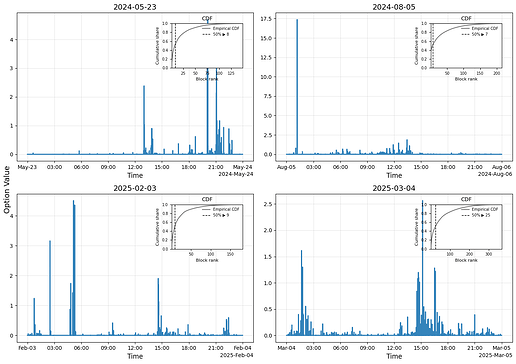
- Extreme days with high option value correspond to days with abnormal volatility: most notably the four largest value (>40ETH per day) dates for option values in our sample, 23 May 2024, 5 August 2024, 3 February 2025, and 4 March 2025 had abnormal intraday ETH price volatility.
The following graphs display daily aggregate option values in ETH.[3]
On high-volatility days, option value is highly concentrated in just a few blocks. For example, on 5 August 2024, only seven blocks generated over 50% of that day’s total option value, only five distinct 1-minute intervals were needed to reach the same threshold.
| Date | p50 | p75 | p99 |
|---|---|---|---|
| 2024-05-23 | 6 | 18 | 88 |
| 2024-08-05 | 5 | 27 | 141 |
| 2025-02-03 | 8 | 19 | 110 |
| 2025-03-04 | 21 | 57 | 234 |
| 1-Minute Bin Counts for 50%, 75%, and 99% of Daily Option Value |
Builders and Orderflow Composition
The next findings are about cross-sectional patterns. First, let’s look at the builder level:
-
There is heterogeneity of profitable exercise across builders. We can group builders into two groups: 1. the (currently market-dominating) builders with valuable non-CEX-DEX flow. 2. builders attached to CEX-DEX-searchers with less valuable non-CEX-DEX flow.
In the second group of builders, the probability of profitable exercise are multiples of that of the other group.
Builder Market Share Option Exercise Probability Titan 29.04% 0.66% Beaverbuild 49.19% 0.75% rsync 16.83% 1.53% tbuilder 0.02% 3.07% blockbeelder 0.09% 9.39%
The differences among builders is mirrored by the TBV composition in the aggregate:
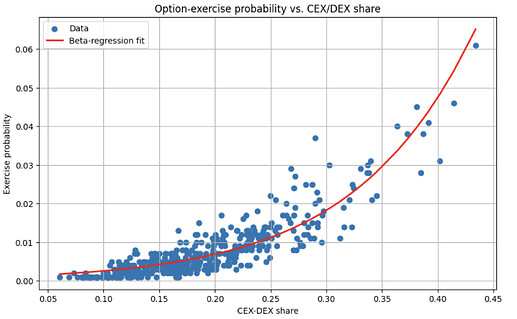
- Most of the relatively low exercise probability can be explained by the dominance of non-CEX-DEX bundles in blocks: in our sample CEX-DEX-flow corresponds to only 20% of total block value.
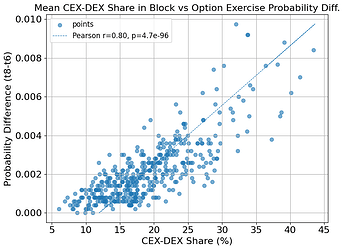
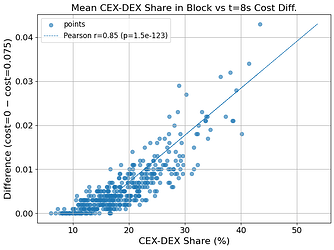
- There is high correlation between days with more CEX-DEX share of TBV and higher option exercise probability: on days where CEX-DEX flow corresponds to more than 25% of total block value, the average exercise probability is 237% higher than the unconditional average. We obtain a strong correlation (0.8455) between the average CEX-DEX-share of TBV and option exercise probabilities:
Shorter Option Time Window and Penalties
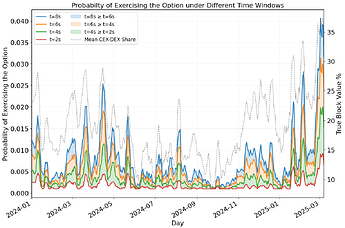
The final group of findings is about mitigation mechanisms. In [1], we proposed two mechanisms: shortening the free option window and punishing builders when they exercise the option by not releasing the blobs. First, we observe that, consistent with theory, shortening the free option window leads to a pronounced decrease in option value and exercise probability:
- Reducing the free option time window from 8s to 6s reduces the average exercise probability by more than 33% on average and the average option value by 36%. Reducing the free option time window from 8s to 4s reduces the exercise probability by more than 50% on average and the average option value by 65%, reducing it from 8s to 2s reduces the average exercise probability by more than 77% and the average option value by 88%.
- The effect of reducing the option time window is very pronounced on the most volatile days in our sample. The following table gives daily aggregate option values in ETH for option time windows of 2,4, 6, and 8 seconds[4]:
| Date | t=8 | 6 | 4 | 2 |
|---|---|---|---|---|
| 2024-05-23 | 41.250462 | 28.048345 | 19.993830 | 6.671739 |
| 2024-08-05 | 48.157314 | 20.266985 | 11.604744 | 2.809852 |
| 2025-02-03 | 46.837631 | 25.756185 | 15.831873 | 5.140573 |
| 2025-03-04 | 40.040843 | 26.432785 | 15.584505 | 5.614737 |
| Daily aggregate option value for different time windows |
| Date | t=8 | 6 | 4 | 2 |
|---|---|---|---|---|
| 2024-05-23 | 0.029 | 0.024 | 0.017 | 0.009 |
| 2024-08-05 | 0.038 | 0.030 | 0.021 | 0.008 |
| 2025-02-03 | 0.031 | 0.023 | 0.015 | 0.008 |
| 2025-03-04 | 0.061 | 0.045 | 0.030 | 0.016 |
| Daily average exercise probability for different time windows |
Moreover, reducing the free option time window reduces the exercise probability drastically in all kind of market regimes including on volatile days:
Next, we look at additional penalties for failures to deliver blobs:
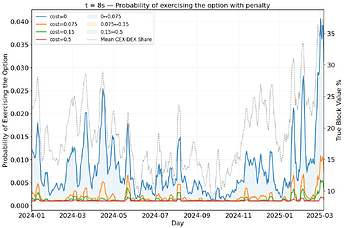
- Introducing penalties for failures to deliver blobs, can reduce the exercise probability drastically. A penalty of 0.5ETH decreases the average option value[5] by 80% and the exercise probability by 90%.
- The effect of penalties is very pronounced on the most volatile days in our sample. The following table gives daily aggregate option values in ETH for no additional penalties and for additional penalties of 0.075ETH, 0.15ETH, and 0.5ETH:
| Date | Cost=0 | 0.075 | 0.15 | 0.5 |
|---|---|---|---|---|
| 2024-05-23 | 41.250462 | 34.180199 | 29.959060 | 20.205566 |
| 2024-08-05 | 48.157314 | 38.128890 | 32.722957 | 22.295733 |
| 2025-02-03 | 46.837631 | 38.675540 | 34.474769 | 23.249300 |
| 2025-03-04 | 40.040843 | 25.869658 | 19.968021 | 8.839374 |
| Daily aggregate option value for different penalties |
| Date | Cost=0 | 0.075 | 0.15 | 0.5 |
|---|---|---|---|---|
| 2024-05-23 | 0.029 | 0.014 | 0.009 | 0.004 |
| 2024-08-05 | 0.038 | 0.016 | 0.01 | 0.003 |
| 2025-02-03 | 0.031 | 0.013 | 0.008 | 0.004 |
| 2025-03-04 | 0.061 | 0.018 | 0.011 | 0.003 |
| Daily avereage exercise probabilites for different penalties |
Moreover, introducing penalties reduces the exercise probability drastically in all kinds of market regimes, for all but the most volatile price swings:
Possible Methodological Shortcomings
Our empirical analysis has several limitations.
- As mentioned before, searchers might size their positions differently if they had a free option and block builders that use the free option will build different blocks. Thus, we likely underestimate the value of the option and the probability of exercising it.
- The dataset covers Ethereum blocks from 8 August 2023 to 7 March 2025 and only those containing CEX-DEX arbitrage in tokens listed on Binance, and so omits trades with tokens not listed on Binance but other CEXs such as Kraken or Gate or other popular DEXs. It also omits trades routed through RFQ, intent mechanisms or other trading protocols.
- We mark the searchers’ position based on the Binance mid-price observed after 8 seconds of the slot, neglecting liquidity and execution costs. Searcher’s might mark them differently.
- For some builders, the stated block value may not fully reflect the value they extract from constructed blocks, because for some non-statistical MEV bundles it might be the case that not the entire value is paid through transaction fees. This gap can distort our estimates of both the exercise probability and the option value for these builders.
- The address heuristics captures only 23 large searchers, missing other CEX-DEX searchers or cross-domain searchers.
- We did not take into account other type of strategies that could use the free option, such as some of the ones mentioned in the bonus section.
In short, future work should incorporate other types of cross-domain MEV, adding more protocols (e.g. UniswapX), searchers, and domains, produce more sophisticated counter-factuals and explore additional strategies.
Interpretation, Recommendations and Conclusion
The above mentioned observations lead to the following preliminary conclusions:
- For realized blocks, the problem is not as severe on average as feared but exhibits high variability, making the problem practically significant on several days in our sample.
- Option value is extremely asymmetrical and a few highly volatile trading days contribute to the majority of total option value. On extreme volatility days, option values are sizeable (>40 ETH daily value) and the share of block where option exercises would be profitable, leading to a significant fraction of empty blocks (3.5-6%). If we want Ethereum to work in a variety of market conditions and not only on average, the free option problem is a real problem even under current market conditions.
- The free option problem in current data is mitigated by the dominance of non-CEX-DEX-arbitrage of total block value. As this MEV is non-stochastic in nature and would be foregone if the option is exercised, it provides a safeguard in situations where exercising the option would be otherwise profitable (just looking at arbitrage bundles). If that share would decrease (e.g. through better application design that make applications leak less MEV), we would expect the free option problem to become significantly worse.
- We observe a lot of heterogeneity in option value and in the probability of exercise across builders. There are builders for which the option would be much more valuable than for others. The currently dominating builders (Titan and Beaverbuild resp. Buildernet) which have a relatively large share of non-statistical MEV, partially derived from exclusive flow, have less of an incentive to use and less value for the free option. Long-tail searcher-builders focused on cross-domain arbitrage have more of an incentive to use and more value for the free option. This might be an indication that in the ePBS world, more CEX-DEX-searchers would place bundles through their own builders on high volatility days, shaking up the current dominance of two large builders.
- Both mitigation mechanisms, shortening the option time window, by moving the two PTC deadlines and the block commitment deadline closer to each other, and additional penalties in case of missed deadlines, would decrease the option exercise probability significantly. However, picking the right PTC deadlines or penalties is not obvious once we also take into account block-inclusion speed and overall throughput. A setting that looks almost optimal under today’s demand may work poorly once market conditions change. In practice, the protocol will likely need a way to retune these parameters over time, either through periodic governance updates or an adaptive, in-protocol feedback rule (e.g., make the cost proportional to the number of unreleased blobs in the last 7,200 blocks).
- Further research is needed to also estimate the value of the option and exercise probability, if builders would factor in the availability of the option when constructing their blocks.
- Further research is also needed to evaluate the impact and trade-offs of potential mitigation mechanisms, such as shortening the option time window or introducing penalties.
Bonus: Known and Unknown Unknowns
We have focused solely on arbitrage trading for our analysis. This is of course only one of many strategies that block builders can use to extract maximal value from the option. What strategies can be used is only bounded by their creativity and the applications that run on chain. Vice versa, the type of applications that can be built on chain are constrained by the possibility of exploits through the free option. We want to point out two fun examples that demonstrate the potential power of the free option beyond arbitrage:
In both this post and the previous one, we examined how the free option lets a block builder wait for off-chain information (for example, price updates) before deciding whether to release or not the block. The same logic extends to any application whose payoff depends on news that may arrive during the 8s window. Imagine a fully on chain prediction market, call it EthMarket, with liquidity comparable to other popular prediction markets. Suppose a highly traded “Which party wins the 2028 US Presidential Election?” contract is about to be influenced by a pivotal news expected sometime in the next few minutes (or hours). A searcher could buy all the liquidity of one side of the contract in a candidate block, then wait until just before the reveal deadline. If either the information is not released or the news are against the trade, exercise the option; otherwise, reveal the block. Because information arrival is stochastic, as long as there is enough liquidity with respect to the information arrival time window, this strategy can be repeated every slot until the news finally lands. With sufficient liquidity, the same pattern could arise around football matches, Elon Musk’s number of tweets, or any other event with an expected important announcement or signals, producing empty blocks on Ethereum whenever external information is imminent. In short, with current ePBS design, Ethereum would not be a friendly layer for a prediction market.
Another strategy consists of multi-block price-spoofing. A proposer for slot n (possibly in collusion with a searcher) first distorts an AMM price in block n-1 by winning that slot’s ePBS auction. The trick works because (i) wallets simulate transactions on the state of block n-1 as soon as its payload is broadcast, and (ii) when the spoofed swap shifts the AMM price, front-ends immediately recompute trade amounts and slippage limits around this new manipulated quote. Between 2 s and 8 s of the next slot, users submit orders that implicitly accept the spoofed price. At the 8 s deadline, the proposer for slot n withholds the blobs, so block n-1 finalises empty; she then sandwiches the mis-priced user flow in her own block n, deterministically when the transactions are public, or probabilistically by sending the sandwich legs to multiple builders when the flow is private. The attack remains profitable as long as enough price-inelastic users trade the affected token(s). Crucially, ePBS makes this tactic even more profitable than in a non-ePBS world, because the proposer can also exploit private order flow without leaking the opportunity to external CEX-DEX searchers who would otherwise arbitrage the spoofed price before the block is finalised. Moreover, in the case that the attacker does not have the option, she has the risk that the trades goes against their spoofing price, making the attack less profitable on average.
The impact of these two strategies is difficult to measure in practice, since it hinges on many factors such as whether a prediction market like EthMarket will ever exist and how front-ends might respond to price-spoofing strategies. It is reasonable to expect that other strategies will emerge in protocols that rely heavily on off-chain information. We do not yet know how many current or future applications will interact with the ePBS free option, but those that do may have to migrate to another venue or redesign their logic less efficiently to neutralise the free option, increasing the burden on developers and exposing users to new MEV strategies. In short, ePBS, with its 8s free option window, carries known and broadly measurable risks along with mitigations for AMM trading. However, for some applications, the impact of this design remains unclear, and it is uncertain whether the available mitigations provide sufficient safeguards.
We construct a counterfactual where the CEX-DEX-searcher is integrated with the builder so that the transfer between the CEX-DEX searcher and the builder needs to be factored out. For the other bundles, there are two possible interpretations consistent with our counterfactual: a) the bundles are by external parties and the builder would lose the payment if he in-validates a block b) the bundles are by the builder or searchers are integrated and the payment is the exact value of the non-statistic MEV bundle. ↩︎
Note that we don’t need to account for the builder bid because we calculate the option value and exercise probability conditional on winning (the option is free since the auction bid is a sunk cost). ↩︎
The cumulative is a sum over the blocks covered by our data set, so that a) some days contain more blocks than others and b) we underestimate daily option value because there probably is value in blocks that our data set doesn’t cover. The graph has similar features, if we consider instead the average over all blocks in the day (multiplied for comparability by the total number of blocks (also those not covered in our data set) per day)
↩︎Reducing block times would probably require lowering the number of blobs per block, unless failing to release a blob does not invalidate the committed block. ↩︎
In this mechanism, if c is the additional penalty, the option value is defined as \max\{-c,v-p+\pi_8\}-(v-p+\pi_8). ↩︎