Abstract
We propose a way to construct distributed block builder networks using a secure knapsack solver. We first attempt to build such a knapsack solver based on dynamic programming techniques. Then, we show how to build such a knapsack solver using a greedy algorithm. We then show benchmarks that provide evidence for pursuing the greedy algorithm approach. Finally, we discuss future research directions for MPC-based block building.
Introduction
Since the introduction of MEV-Boost, block builders have made hundreds of ETH. However, it is clear that the winning builders are starting to centralize amongst a top few. This phenomenon can potentially lead to centralization in the future. As such, there has been some thoughts on how to potentially decentralize the block building process.
The Flashbots team, as part of their research into SUAVE, has recently shared MEV-share, a potential building block ![]() that can be used towards building decentralized builder networks. However, it relies on a new entity, matchmakers, in order to work. As such, there is still a lot of work to be done to start working towards this problem.
that can be used towards building decentralized builder networks. However, it relies on a new entity, matchmakers, in order to work. As such, there is still a lot of work to be done to start working towards this problem.
At HashCloak, we have been working on ways to add privacy to various parts of Flashbots products. Recently, we realized that block building is an instance of the knapsack problem. As a result, a simplified form of block building can be solved using well-known off-the-shelf algorithms from computer science. Using this fact, we describe a way to build a privacy-preserving builder network using multiparty computation.
In this post, we go over briefly how block builders construct blocks, knapsack problems and applications of the knapsack problems to auctions. Then go over how to construct privacy preserving knapsack auctions using MPC. Finally, we include a discussion on the implementation challenges and directions for future research.
Primer on Block Builders
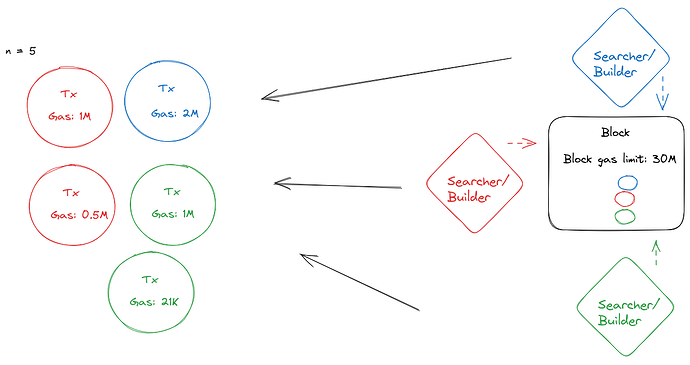
Block builders are entities that are in charge of constructing profitable blocks for block proposers. They are in charge of ensuring that the transaction orderflow from various sources (e.g. searchers, private mempools, public mempools, etc) is profitable and executable (i.e. ensuring that all the transaction bundles sent by searchers are valid Ethereum transactions that operate within the block gas limit).
The way in which block builders decide which transactions to include in their block is highly specific to each block builder. Many rely on the open source implementation by Flashbots, others build their own block builders with their own heuristics. The most common ways to include transactions into blocks are
- First come, first serve (FCFS): The first transaction that the block builder receives gets included first
- Auctions: Block builders will auction off space in their blocks using common auction designs such as first price auctions, english auctions, etc
- Greedy algorithms: Block builders may simply chose the most profitable transactions in a given timeframe to include in their blocks.
As such, there isn’t one canonical way to include transactions into blocks.
Desiderata for decentralized builder networks
Before diving into our solution to building decentralized builder networks, we go over some potential desirable criteria for an ideal decentralized builder network:
- Scalable: An ideal block builder network design should potentially account for thousands of searchers and builders.
- Private: No entity should know what transactions are going to be included in a block
- Fair: No entity should know the result of the block ahead of anyone else
- Permissionless: Anyone should be able to become a block builder (within reason obviously
 )
) - Profitable: A builder participating in a builder network should be able to make a profit
- Hides residual bids: Residual bids are partially filled or unsuccessful bids done in an decentralized auction. Any block builder network that has some form of auction should not reveal whether a particular set of transactions make it into the block until the block is included in the blockchain and only the bidder knows that their transactions didn’t make the block.
Primer on Knapsack Variants
The knapsack problem is the problem of trying to fit in as many items into a knapsack as possible given several constraints on both the items and the size of the knapsack. Many different instances appear throughout computer science such as the 0-1 knapsack problem, multidimentional knapsack problem, and the fractional knapsack problem. As it pertains to decentralized block builder networks, the 0-1 knapsack problem is the most relevant knapsack variant.
The 0-1 knapsack problem is formally defined as follows:
Given items i_1,i_2,i_3,...i_n with values v_1,v_2,v_3,..,v_n and weights w_1,w_2,w_3,..,w_n, and each item is either included or not, denoted by x_i and a knapsack of size W, we need to find solutions to the following optimization problem
There are two well-known ways for solving this variant of the knapsack problem. Namely, dynamic programming and a greedy algorithm. We will go into both of those approaches later on in this post. Since the Knapsack problem is NP-hard, both approaches forgo either optimality or being able to run in polynomial time with large enough instances.
Knapsack Auctions
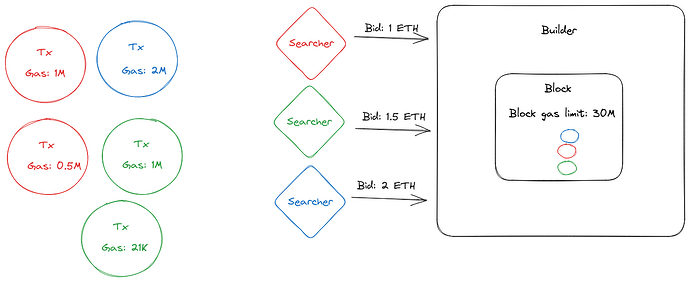
Based on the general description of the knapsack problem, we can reformulate it in order to turn it into an auction-style problem. A knapsack auction is an auction in which bidders with bids b_i for an item with weight w_i are trying to get space in a seller’s knapsack of maximal weight W. Formally,
the seller is trying to maximize \sum _{i=1}^{n}v_{i}x_{i} \leq W. In the case of block building, each bidder can be considered a searcher with MEV opportunities that wants to get their transaction bundles that cost w_i gas to execute in a block of maximum W gas.
For any auction mechanism, we want the following properties:
- A DSIC auction: Dominant strategy, incentive compatible
- Maximizes the surplus: In our case, maximizes the profit that can be gained in a maximal
Wgas block - Runs in polynomial time
Due to impossibility results in algorithmic game theory, one needs to forgo either 2 or 3. The relevant solutions correspond to the well-known solutions provided by dynamic programming and a greedy algorithm, both of which we will go over in this post. For a more detailed description about the proofs, read Tim Roughgarden’s lecture notes on the topic.
Approaches
Now, we are ready to go into more details about how to go about constructing secure knapsack auctions by first explaining the vanilla dynamic programming solution. Then we will go into details about the greedy algorithm approach. Finally, we will compare and constrast both for our use case of distribute block building networks.
A first approach: Dynamic Programming
The most common approach for solving the 0-1 knapsack problem is via dynamic programming. Dynamic programming is an approach that first starts by solving smaller instances of the knapsack problem, stores their solutions in a table and then slowly builds up into the full problem instance. This approach always leads to an optimal solution for the 0-1 knapsack problem. A more detailed description can be found here.
The dynamic programming method for solving the 0-1 knapsack problem takes O(nW) time and O(nW) storage, in its naive form. If one adds extra assumptions about the items and their sizes, it is possible to reduce the storage complexity to O(W). As such, if the number of items is large or the weight is large, it may not be feasible to run the dynamic programming solver in polynomial time.
A second approach: Greedy Algorithm
As the knapsack problem is NP-hard, another common way to solve it is to use approximation algorithms. So, instead of finding the optimal solution, an approximate solution is found instead. In particular, greedy algorithms are a common approximation algorithm used to solve the knapsack problem.
For the 0-1 knapsack problem, it is well-known that greedy algorithms don’t find an optimal solution. However, there are 1/2 approximation greedy algorithms i.e. algorithms that guarantee that a solution is within a factor of 1/2 of an optimal solution. A more detailed discussion can be found here.
Compared to the dynamic programming solver, another advantage of the greedy algorithm solver is that its runtime is O(nlogn) and its storage complexity is O(n) where n is the number of items in the knapsack. As such, it doesn’t depend on how large the knapsack can be which in practice, can make the greedy algorithm a more practical algorithm to use with larger knapsack sizes (e.g. blocks in Ethereum)
Why MPC?
We’ve gone over very high-level primers on the 0-1 knapsack problem, its corresponding applications to combinatorial auctions and solutions to conducting knapsack auctions. However, in decentralized block building, we are dealing with entities that care about the privacy of their transaction bundles and the privacy of their bids to get these bundles included. As such, any auction mechanism will need to take this into account.
Before going into short primer on secure optimization and secure auctions, we should motivate the need for multiparty computation (MPC). The reasons for using MPC over other privacy-enhancing tech (PET) are the following
- We need to actually compute a result (e.g. number, list) given inputs that no one but the participants know. Zero-knowledge proofs (ZKPs) gives us proofs which are useful to telling us that the result was computed correctly and can be independently verified but it doesn’t give us the final result. FHE allows the same functionality as MPC but with the key distinction of being in the single server setting instead of a multi-party setting. SGX is able to provide this functionality but one has to rely on Intel’s hardware assurances and have access to an SGX server.
- We need a way for multiple different parties to compute this result. The area of collaborative ZKPs is nascent for general purpose variants but as discussed in the previous bulletpoint, ZKPs don’t provide the functionality that we need. As for FHE, threshold FHE is simply a subset of MPC functionality. Finally, for SGX, the most common ways to have several nodes run the same computation is by sharing the same enclave binary. However, SGX is known for being susceptible to a wide range of practical side channel attacks. Further, due to the reliance on the honesty of Intel as the manufacturer, SGX doesn’t give us cryptographic guarantees of security but instead an economic one.
| PET | Pre-execution Privacy | Failed execution Privacy | Post-execution Privacy | Natural notion of multiparty? | Returns result of computation? |
|---|---|---|---|---|---|
| MPC | ✓ | ✓ | ✓ | ✓ | ✓ |
| ZKP | ✓ | ✓ | ✗ | ✗ | ✗ |
| FHE | ✓ | ✓ | ✓ | ✗ | ✓ |
| SGX | ✓ | ✓ | ✓ | ✓ | ✓ |
In order to ensure that the sensitive data used to construct these blocks via the knapsack problem is still private, we need some form of privacy enhancing technology. As we need to have a set of mutually distrusting parties contribute to the construction of a single block, multiparty computation (MPC) is the best primitive for this given our constraints.
Optimization Problems and auctions in MPC
A significant amount of research has been devoted to the development of privacy-preserving auctions and combinatorial optimization problems within the realm of Multi-Party Computation (MPC). This exploration mainly centers around the construction of secure auctions for various commodities markets, such as electricity. These are often adaptations of the max-flow/min-cut optimization problem and associated graph-based optimization problems.
In the context of graph theory applications, MPC is generally employed as a blackbox. These applications primarily revolve around secure combinatorial problems over graphs, where the focus lies in concealing the graph’s structure. This is achieved by deploying data oblivious techniques, which maintain the privacy of the involved participants.
An interesting aspect of this research is that, despite the extensive work on graph-based optimization problems, there appears to be a lack of exploration when it comes to the knapsack problem. No substantial work has yet focused on creating secure variants of its solutions. This gap presents an intriguing area for further study and development within the field of MPC.
When we turn to the domain of secure combinatorial auctions, the emphasis shifts towards the design of specialized algorithms, rather than relying solely on blackbox constructions. These unique algorithmic constructions are designed to work in tandem with a combinatorial optimization problem. Consequently, they primarily concentrate on the integral aspects of the auctions, such as bid calculation and the distribution of final results amongst participants.
For a more comprehensive and detailed understanding of the current state of secure optimization constructions, Abdelrahaman Aly’s PhD thesis serves as an excellent resource. His work offers a deep dive into the intricate details of this emerging field.
Implementation and empirical results
Since there are no special purpose MPC protocols for variants of the knapsack problem, we leveraged the general purpose MP-SPDZ framework to first benchmark a naive implementation of two knapsack variants: 0-1 knapsack and knapsack auctions.
We make several simplifying assumptions in our implementations:
- The players (n=10) are both a searcher and a builder. A more realistic implementation would instead follow a different architecture similar to the one used here.
- All the clients run on the same machine. A more realistic implementation would have this be distributed across different machines
- Doesn’t take into account fairness. It is a open question as to what fair MPC protocol to use
- All transactions are conflict free. In other words, we assume that transactions don’t have any conflicts in terms state access as we only use the information in a block necessarily for calculating profitability.
Dynamic Programming-based Knapsack Solver
The 0-1 knapsack solver used is the simple dynamic programming based solver described here and can be found here.
The setup is as follows:
- W is the maximal block gas limit. For example, on the main Ethereum chain, this is 30M
- n is the number of transactions to be included in a block.
- Weights are the gas costs for each transaction.
- Values are the amounts to be paid in profit for each transaction.
- Each builder is an MPC node that contributes sets of transactions to be potentially included in a block.
In order to make this dynamic programming solver more privacy-preserving, we need to ensure the following:
- Data accesses in the table are oblivious. In the dynamic programming algorithm presented earlier, array acceses are dependent on secret values, namely the number of transactions to be considered for addition.
- Minimize data leakage during the computation of maximal values.
- Minimize data leakage during conditional assignments
In our implementation, we addressed the previous points as follows:
- Used oblivious RAM (ORAM) in order to hide the access patterns
- Used secret-shared values for all arithmetic operations
- Used privacy-preserving conditional assignments to do conditionals over secret-shared data
Issues with our implementation
However, due to several limitations of MP-SPDZ, we had to have both the maximal weight and the number of transactions be public integers as these values are known at compile time but secret-shared values are not known at compile time.
Other issues we encountered with our dynamic-programming based solver is that our simulated inputs (found in simulate_data.py) which attempt to provide realistic looking inputs are too large to run in an MPC environment. In particular, with maximal weight of 30M (as per the current block gas limit in Ethereum) and 34 transactions, we ran out of memory and storage. The ORAM storage gets very large as the storage size of a function of maximum weight and number of items. As a result, each party would need nearly 1 TB of RAM in order to do the computation. For more details about this issue in relation to our implementation, read this response from the author of MP-SPDZ.
Greedy-based knapsack solver with auctions
For the greedy 1/2 approximation, we implemented the algorithm described here in section 2.2 and its implementation can be found here.
The setup is the following:
- Each builder has a corresponding bid in addition to their transaction bundles.
- Each bid is the amount a builder is willing to pay to take up a certain about of block space denotes in terms of gas
- W, the maximal weight, is the block gas limit
In order to make this greedy solver more privacy-preserving, we need to ensure the following:
- Sorting the bidders is done obliviously regardless of the condition.
- At each iteration of the greedy algorithm, the conflict checking should be done obliviously. In other words, we shouldn’t know which bidder gets added to the greedy set.
In our implementation, we did the following along with some workarounds MP-SPDZ’s functionality to ensure minimal leakage:
- Usage of secret-shared variables in order to do secure computation
- Usage of oblivious sorting to sort the initial bids list by
b_i/w_i
Results
Unlike the dynamic programming solver, since this greedy solver is a 1/2 approximation, it can be run in polynomial time. As such, we were able to compile and run the program in an MPC environment.
We ran benchmarks in four settings:
- an unoptimized knapsack auction compilation: This just uses the default compiler configuration in MP-SPDZ
- a compiler optimized version that prioritizes faster compilation of repeated operations over potential increased communication rounds, by simplifying complex parallel computations: This is enabled by using
-Cin MP-SPDZ during compilation - an daBits optimized knapsack auction: This is enabled by using
-Xin MP-SPDZ during compilation - an edaBits optimized knapsack auction: This is enabled using
-Yin MP-SPDZ during compilation
daBits and edaBits are protocols for generating mixed circuits. These protocols allows one to switch between arithmetic and binary circuits in order to leverage the strengths of each kind of circuit. In particular, for secure airithmetic and other linear functions, these protocols allows for switching to an arithmetic circuit and for non-linear functionality such as comparisons, it allows for switching to a binary circuit.
All benchmarks were ran on a single machine (Lenovo E15 with 16 GB of RAM on an 11th Gen Intel i7 processor) using the maliciously secure shamir secret sharing protocol. For more details on how to replicate these numbers, please read this folder
| Compilation Mode | Time (in seconds) | Rounds | Global Data sent (in MB) |
|---|---|---|---|
| Unoptimized optimized Greedy Knapsack Auction | 2244.1 | 174018 | 821060 |
| Compiler optimized Greedy Knapsack Auction | 2137.38 | 174018 | 821060 |
| daBits Optimized Greedy Knapsack Auction | 2120.96 | 174018 | 821061 |
| edaBits Optimized Greedy Knapsack Auction | 2116.21 | 174018 | 821061 |
Issues with our implementation
We summarize our challenges in using the MP-SPDZ MPC framework for implementing a secure greedy knapsack algorithm:
-
Creating a Custom Type for Holding Bidder Information: A challenge arose in creating a custom type within the MP-SPDZ framework to hold and manage bidder information securely. This involved defining a class object with MP-SPDZ types that could efficiently handle the sensitive bidder data. Integrating and ensuring the correct functionality of this custom type added complexity to the implementation.
-
Conditional Assignments for the Greedy Condition: Enforcing the greedy condition in the knapsack algorithm required the use of conditional assignments. These assignments ensure that the maximum capacity is not exceeded while adding new bidders to the greedy list. Implementing conditional assignments in the context of secure multiparty computation using MP-SPDZ requires careful handling to maintain security guarantees and prevent potential vulnerabilities.
-
Secrecy of Winners Until the End: Ensuring the confidentiality of the auction winners until the end of the computation posed another challenge. It was crucial to design the implementation in a way that the outcome and identities of the winners remained secret during the execution of the algorithm. Preserving secrecy and preventing any leakage of sensitive information required additional measures and careful consideration throughout the implementation process.
Discussion
While the experiments shown here assume very simplified environments of what would happen in practice, it is clear that the greedy approach for building blocks is a promising direction to go into. Not only does its runtime and storage complexity make it more suited for the blockbuilding domain, but it is also better suited for real-time computation. This latter point is of significant importance, considering the specific characteristics of blockchain systems.
In the context of blockchain systems, such as Ethereum, several factors contribute to the need for real-time decision-making and optimization. Firstly, the number of different state transitions of the Ethereum Virtual Machine (EVM) given the current Ethereum state and a set of prospective transactions is intractable. Secondly, blocks are accepted and finalized quite quickly in Ethereum, leaving a limited window for decision-making. Lastly, miner extractable value (MEV) opportunities expire rapidly, necessitating prompt action to capitalize on them.
These factors require making decisions as they arise and making optimal decisions based on real-time information. In this context, the use of dynamic programming solvers, which would enable finding the best overall decision, becomes impractical. The efficiency and speed of the greedy approach become appealing for addressing these time-sensitive requirements.
The experiments conducted in this study made heavy use of a general MPC framework, which provides a baseline for evaluating the practical efficiency of such a system. However, considering the specific needs of a greedy-based knapsack auction in the blockchain domain, it is worthwhile to explore the development of a special-purpose MPC protocol. A dedicated protocol tailored to the requirements of the greedy algorithm may offer further improvements in terms of both communication and computational complexity, as it would eliminate the overhead associated with a general-purpose MPC framework.
When choosing the appropriate MPC protocol, it is important to consider the tradeoffs between security models and practical efficiency. The choice of security model will have implications for the computational and communication gains achieved. Based on our benchmarks, assuming honest behavior on the part of the participants provides better computational and communication gains, while assuming more pessimistic behaviors may introduce efficiency drawbacks. However, the choice of security model should also reflect the expected behaviors and threat models associated with block building and searching.
Considering the real-world behavior of searchers and builders, a promising approach may be to employ a maliciously secure protocol in the honest majority setting. This allows for stronger security guarantees while still maintaining practical efficiency. However, depending on the specific deployment scenario, assuming a semi-honest model might also be worth considering, as it can offer certain practical advantages.
By carefully considering the tradeoffs between security models, practical efficiency, and the specific requirements of the greedy-based knapsack auction, blockchain systems can make informed decisions when selecting the appropriate MPC protocol. This will enable them to leverage the advantages offered by the greedy algorithm for efficient block building, while ensuring the desired level of security and efficiency in practice.
Future Research Directions
While our results are just the tip of the iceberg of what is possible in the design landscape of building decentralized builder networks, we wanted to leave the reader with a few more research directions that this work edges us towards.
More complex greedy conditions
In this research, we mainly focused on a single factor for determining inclusion and profitability into a block, the block gas limit. However, in practice, there are many other factors that go into deciding what transactions to include in a block such as the interdependence between transactions against the state, the amount of MEV a certain set of transactions have, using flashbots’ bundle scoring mechanism etc.
This leaves the door open to exploring MPC-friendly greedy conditions that better express preferences for bundle inclusion. Protocols like MEV-share have the potential to be MPC-friendly.
Incentives
Having a distributed builder network leads to questions about how each builder participating in the network will be able to make money off of building blocks. The MPC design presented here is quite nice in that it should be possible to add privacy-preserving revenue distribution in addition to doing an auction.
Work by Tim Roughgarden and Shi, Chung and Wu give interesting results on how incentives play into transaction fee market design with implications to block construction. In particular, the work of Shi, Chung and Wu allude to improved incentive compatibility when an MPC model is assumed for the participants in a transaction fee market. Further, in addition to their work, it should be possible to integrate better cryptoeconomic guarantees in order to relax several a few cryptographic security assumptions.
Acknowledgements
Thank you to Johnathan Passerat-Palmbach, Tina Zhen, Alex Obadia, Thomas Steeger, Ghilia Weldesselasie, Hernan Dario Vanegas Madrigal, Urie, Andrew Miller, Kobi Gurkan, Jonatan Luther-Bergquist, and Abdelrahaman Aly.