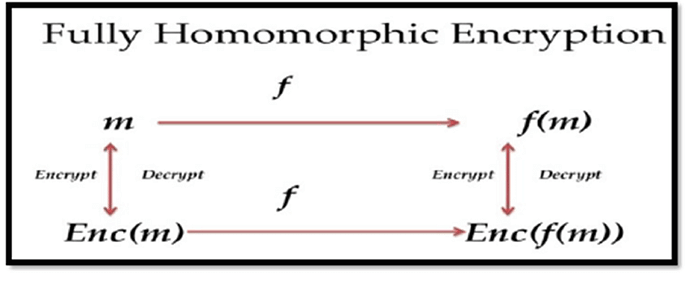
Fully Homomorphic Encryption (FHE) boasts a rich history in cryptography, earning its name from its distinctive ability to perform computations directly on encrypted data without exposing the original content.
As illustrated in the diagram below, the fundamental principle of FHE is that the same operation f can be applied to both the plaintext m and its encrypted version Enc(m), yielding consistent results. Specifically, the data m is encrypted into Enc(m) using the secret key sk held by the user before being sent to a third-party computation node. The node then returns the result of Enc(f(m)), which the user can decrypt using their secret key sk to obtain the final result.
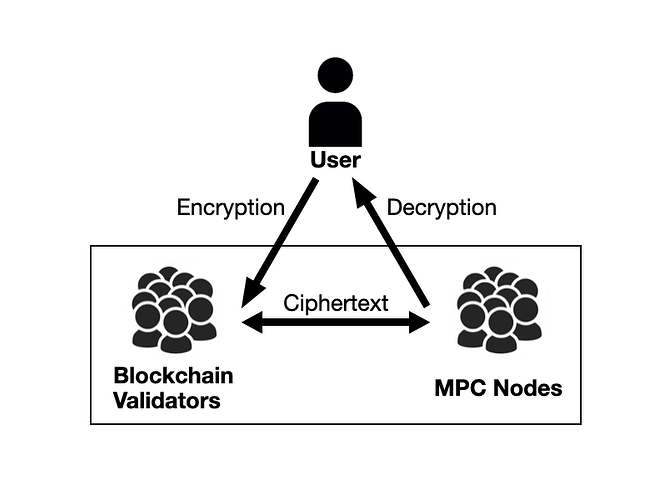
When FHE is employed to build a confidential blockchain network, the need for different users to opt into the same open ledger—such as participating in a trading pool—requires that the secret key sk used to encrypt data be shared globally. To safeguard this key from compromise, most FHE-based blockchain networks introduce a threshold signature-based MPC network to manage the key. As illustrated in the diagram below:
- The key is either distributed among MPC nodes or generated dynamically through Distributed Key Generation (DKG).
- Data encrypted by users with the global public key, and then forwarded to validators (FHE computation nodes) for processing.
- The results of the computations can only be read by users after being decrypted by the MPC network.
There are several drawbacks in the current design, but TEE can be used to improve it across multiple dimensions
- Key Security
Introducing MPC to manage the key is a common method; however, there is a theoretical risk of collusion between MPC nodes. While increasing the number of nodes can mitigate this risk, it also introduces more latency. An effective alternative is to run MPC nodes inside a TEE (such as Intel SGX), where the program can be proven immutable and access is restricted. This approach essentially treats TEE as a form of two-factor authentication (2FA). For more details, you can check out this post I published earlier on the Ethereum research forum.
- Encryption/decryption Validity
Currently, we cannot guarantee the integrity of the plaintext during both encryption and decryption step, especially for the progress of decryption, which is outsourced to the MPC network in most of the implementations. To address this issue, we can introduce ZKP during encryption and decryption.
As for FHE encryption, it has been implemented by projects like Zama’s tfhe-rs and PSE Greco, where the ZKP accompanying the encrypted data can be verified by the computation node. While this is practical due to the acceptable cost of proving encryption with zero-knowledge circuits, do we really need to generate a ZKP for each piece of encrypted data?
The complication of implementing ZKP for decryption in MPC network also makes it hard to land on the ground in a short-term, an alternative approach is to run the MPC nodes inside a TEE, which can solve both key security and decryption integrity issues simultaneously, and with lower computational cost.
- Computation Validity
FHE itself guarantees that the result of a computation applied to ciphertext is the same as if the computation were applied to plaintext. However, it does not guarantee that the computation logic is what we expect. For instance, if we want to compute a + b, we expect the computation node to execute Enc(a) + Enc(b) in the circuit. Theoretically, though, the computation node could return Enc(a) * Enc(b), and if we don’t know what the actual a + b should be when we receive the result, we cannot verify if the result is as expected.
In FHE-based blockchain networks, we can avoid this issue by using a consensus algorithm, where multiple nodes perform the computation simultaneously. However, this leads to redundancy in FHE computation. Another cryptographic approach is to produce a ZKP during the computation and return it along with the encrypted computation result, allowing anyone to verify that the encrypted result was computed as expected. Zama is working on implementing a ZK circuit for the bootstrapping phase using zk-SNARK during computation. However, benchmark results show that it still has a long way to go (as illustrated in the table below, it takes nearly 20 minutes to prove a single bootstrapping step on a machine with 192 cores and 768GB of memory).
| System | Prover Time (min) | Verifier Time (ms) |
|---|---|---|
| M2 MacBook Pro - 8 cores, 24GB | 48 | 5 |
| Hpc7a.96xlarge - 192 cores, 768GB | 18 | 8 |
Considering that, with almost the same hardware, a single integer operation takes less than 200ms (see full benchmarking here), do we really need to incur such high costs to achieve computation validity? I don’t think so, at least not in the short to mid term, as it is not practical. In this scenario, we can introduce TEE as a trusted container, where the full FHE computation node runs inside trusted hardware, like SGX. We can achieve computation validity by protecting the program from being compromised by any other parties. While we don’t have benchmarks for running the node inside TEE yet, it will obviously be far more efficient than producing ZKP.
Conslusion
By posting this here, I hope to raise awareness about the drawbacks present in current FHE-based blockchain systems. We should seriously consider using TEE to address these issues, as it is the most effective solution I have encountered from an engineering design perspective.