Authors: @saguillo2000, Lucianna Kiffer, Vahid Ghafouri, Guillermo Suarez
Arxiv Link: [2508.03474] Unravelling the Probabilistic Forest: Arbitrage in Prediction Markets
TL;DR
Polymarket’s binary-condition design enables three forms of arbitrage: two types of Rebalancing Arbitrage within a single market (of one or more conditions), and Combinatorial Arbitrage across markets.
We compute that the total amount extracted using these strategies is approximately $40 million over one year of data, from April 1, 2024, to April 1, 2025.
Background
Polymarket is a prediction market platform that allows users to speculate on the outcomes of future events by trading shares tied to specific outcomes. Polymarket is built on top of the Polygon blockchain, providing some decentralized properties to the platform (i.e., users own their positions and can settle on-chain, though bid matching remains centralized). Each condition poses a question about a future event, such as “Will team A defeat team B in the big game?”. Users can buy shares (or tokens) in “YES” (the condition will become true) or “NO” (the condition will not become true) outcomes, with share prices fluctuating based on market demand and reflecting the collective belief about the likelihood of each outcome.
A market is thus a future event associated with one or more conditions. For example, consider the question, “Who will win the Team A vs. Team B match?”. In this case, the market would include three conditions:
(1) Team A wins,
(2) the match ends in a tie, or
(3) Team B wins.
Each condition is represented by a binary token indicating whether the condition is true or false. To ensure proper resolution, the set of conditions must be exhaustive, collectively covering all possible outcomes of the event, and independent, where only one condition can resolve to true.
Types of Arbitrage
We define two types of arbitrage strategies:
-
Market Rebalancing Arbitrage, which occurs within a single market.
-
Combinatorial Arbitrage, which occurs across multiple markets.
(1) Market Rebalancing Arbitrage
Single-Condition Arbitrage
With the current bidding system, the following scenario can occur:
Suppose there is a market predicting whether Trump will be president in 2024. You can buy either YES tokens (he will) or NO tokens (he won’t).
Since pricing of the two tokens is handled separately, it’s possible for YES to trade at 0.50 and NO at 0.47. By design, the sum of both prices should equal 1. In this case, there is an arbitrage opportunity: by buying both tokens at the given price and holding, once the market resolves, you would capture the difference — in this example, 3%. This is an example of a long position.
A similar situation arises if YES is valued at 0.50 and NO at 0.55. In that case, you can provide liquidity for both tokens, securing an extra 5% yield. This is an example of a short position.
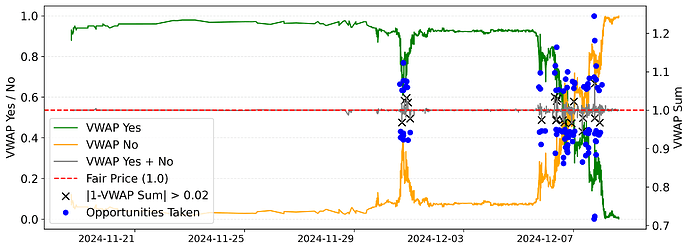
Below we show how these opportunities look like over time with a market capturing whether Assad would remain president of Syria. We see that for the majority of the market duration, the YES position held at over .90, with the market flipping in early December with rebel forces seizing Damascus. The black x’s show when arbitrage opportunities existed in this market with a margin of more than $0.02 profit per Dollar (from a weighted average of prices from executed bids). Given historical bid data, we also find players who purchased (or sold) both tokens at a guaranteed profit. We see that these opportunities exist at times of uncertainty in the market, and that our estimates of profit generally undercount the potential arbitrage profit players are able to execute.
Market behavior visualization for the condition: “Will Assad remain President of Syria through 2024?”
Over all single-condition markets during our measurement period, we calculate that the total profit extracted with the single condition strategy was:
| Strategy | Direction | Total Profit (USD) |
|---|---|---|
| Single Condition | Long | $5,899,287.43 |
| Single Condition | Short | $4,682,074.77 |
Multiple-Condition Arbitrage
Consider a market with three conditions: who will win the 2024 election — Trump, Biden, or another candidate. You can buy YES tokens for each outcome (YES-Trump, YES-Biden, YES-Other).
By design, the total price of all YES tokens should add up to 1. But imagine this situation:
-
YES-Trump = 0.40
-
YES-Biden = 0.35
-
YES-Other = 0.20
Here, the sum is 0.95. Since it’s less than 1, there is a long opportunity: you can buy all three tokens for less than their combined guaranteed payout of 1, locking in a 5% gain.
On the other hand, if the prices were:
-
YES-Trump = 0.45
-
YES-Biden = 0.40
-
YES-Other = 0.20
The sum would be 1.05. In this case, the short strategy applies: by selling exposure to all three tokens, you secure a 5% return.
For NO tokens, the rule flips. In a 3-condition market, the sum of all NO token prices should equal (N - 1) = 2.
-
If the total is less than 2, you can go long on NO tokens.
-
If it’s greater than 2, a short position will yield a profit.
The total profit extracted in our measurement period within markets with multiple conditions was:
| Direction | Token Type | Total Profit (USD) |
|---|---|---|
| Long | YES | $11,092,286.31 |
| Short | YES | $612,188.83 |
| Long | NO | $17,307,113.81 |
| Short | NO | $4,264.33 |
(2) Combinatorial Arbitrage
We now consider two linked markets about the same election and their conditions.
-
Market M1 (Winner):
-
Democrats win (M1–S1)
-
Republicans win (M1–S2)
-
Market M2 (Winning margin, partitioned into buckets):
-
D by 0–5 pts
-
D by 5–10 pts
-
D by 10+ pts
-
R by 0–5 pts
-
R by 5–10 pts
-
R by 10+ pts
By logic, if Democrats win in M1, the true outcome in M2 must be one of the D margin buckets; if Republicans win, it must be one of the R margin buckets.
Suppose current YES prices are:
-
M1 (Winner)
-
Democrats win = 0.48
-
Republicans win = 0.52 (notice M1 sums to 1.00 one would expect)
-
M2 (Margins)
-
D 0–5 = 0.35, D 5–10 = 0.15, D 10+ = 0.10 → D total 0.6
-
R 0–5 = 0.20, R 5–10 = 0.10, R 10+ = 0.10 → R total 0.4
These markets are dependent but priced inconsistently. That opens a combinatorial arbitrage:
Portfolio (guaranteed to hit at least one winner):
-
Buy YES–Democrats win in M1 for 0.48, and
-
Buy all four Republican margin YESs in M2 for 0.4 total.
Why this guarantees a win
-
If Democrats win, your M1 ticket pays 1.
-
If Republicans win, some R margin bucket must occur, so one of your M2 R tickets pays 1.
Cost vs. payoff
-
Total cost = 0.48 + 0.4 = 0.88
-
Guaranteed payout = 1.00
-
Locked-in profit = 0.12 (13.63% profit)
This is the essence of combinatorial arbitrage: use the logical links between markets (e.g. winner ↔ margin buckets) to cover every possible world with overlapping bets, so at least one side must pay out. The opportunity exists because the cross-market prices don’t add up coherently (here, M1 is rich on “Republicans win,” while M2 underprices the sum of all Republican margins).
We find all pairs of markets with this conditional dependency (i.e., the outcome of either determines the outcome of the other). We find 11 such pairs where arbitrage opportunities existed (all relating to the U.S. 2024 election). Only 4 of these pairs had arbitrage extracted via the combinatorial condition strategy, with a total profit detected as:
| Pair | Total Profit (USD) |
|---|---|
| Pair 1 | $15,818.53 |
| Pair 2 | $60,236.71 |
| Pair 3 | $629.16 |
| Pair 4 | $18,472.31 |
Check out our paper for formal definitions of these strategies and our full analysis. [2508.03474] Unravelling the Probabilistic Forest: Arbitrage in Prediction Markets
Wrapping up and Open Questions
In this project, we focused on arbitrage between strictly dependent conditions. Within a single market, that’s straightforward: conditions are exhaustive by definition, so rebalancing creates guaranteed profit opportunities. Between markets, we only counted strict dependencies that lock in profit no matter what happens. That leaves plenty of room for looser definitions—like one-directional dependencies—or more nuanced strategies, such as hedging and partial exits.
When measuring realized arbitrage, we required evidence that a trader actually bought all the needed positions at the right prices. We then computed the profit as the guaranteed return if they held until resolution. Of course, holding comes with opportunity cost and liquidity constraints, so these numbers represent an upper bound on extractable profit, not what was actually pocketed in practice.
Looking ahead, a few big questions stand out:
-
Market relationships: How do we detect subtler dependencies across markets, beyond strict overlaps?
-
Risk and realism: What changes if traders hedge, exit early, or rebalance dynamically instead of holding to resolution?
-
Inefficiency vs. discovery: Which arbitrages are real mistakes, and which are just markets catching up to new information?
Finally, mapping these obvious arbitrages isn’t just about quantifying profit—it’s also about protecting less strategic users. If simple, structural inefficiencies exist, they can be consistently exploited by sophisticated players at the expense of newcomers. Understanding and exposing these patterns is a first step toward making prediction markets fairer and more robust.