A lot of discussion around MEV touches on the idea of transaction ordering. An idealised and simplified view of block building is that of a function which maps an unordered set of transactions, T, to some outcome, denoted r(T), which often takes the form of an ordered list of transactions. We can think of such a function as an ordering rule. This post explores approaches to enforcing ordering rules (without commenting on which rules are desirable) with the aim of placing ordering regimes in context relative to each other and to explore the space to possible rules and enforcement mechanisms (so please add if I missed anything)
Note: to be pedantic, some ordering rules are mappings from sets of transactions to sets of ordered lists - i.e. there are multiple allowed orderings to choose from for a given input, so r(T) is a set.
I have attempted to categorise approaches to enforcing block ordering rules according to the properties of the rule. Some examples I provide might seem as if they are very application specific or provide narrow guarantees. These should not be discounted as it may be possible to compose multiple rules on block building (and outside of block building) to provide desired guarantees across a range of applications. For example, censorship resistance might be handled by a different mechanism than the ordering rule(s). Similarly, one may have rules specific to the execution of certain applications, although work needs to be done to show that composed rules maintain the properties they have in isolation.
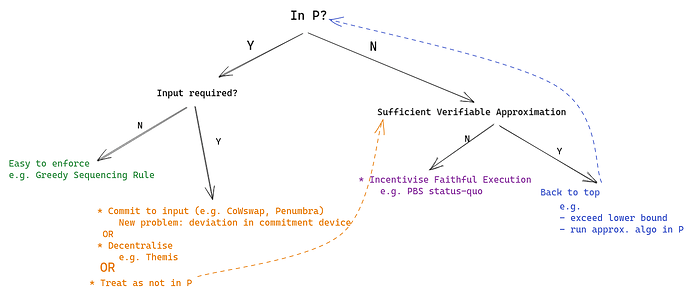
Q1: Is the rule in P?
I’d like to segment ordering rules into those which are in P and those which are not. The motivation behind this is that we cannot reasonably expect builders to execute rules which are not in P due to computational complexity and the plans for blockchain networks to scale to process thousands of transactions per second. A rule, r, is said to be in P iff we have a set of tuples, R:= \{(T,y)|\forall T\forall y\in r(T)\} and for a given input set T we can deterministically find y' such that (T,y')\in R or return \bot if no such y' exists, in polynomial time. For simplicity’s sake I omit reference to randomised rules and algorithms, but there certainly is room for extension to rules which are in RP or rules that require a certain probability distribution over potential orderings. You could also argue that I should also look at NP in general, since we can restrict the size of the input so non-polynomial time algorithms are on the cards.

Q2.1: Given that a rule is in P, can we tell if (x, y)\in R by only looking at y?
In other words, can we look only at the block and tell if the rule was followed without knowing what the input was. Such a rule might seem trivial at first, but an example below might help illustrate why its a meaningful category.
Yes, we do not need the input to know if the block is valid according to r
An example of such a rule is the Greedy Sequencing Rule (Ferreira & Parkes). Whereas the rule given in the paper does actually require knowledge of the input to verify that an ordering of transactions is valid, the rule has the property that if for ordering y \exists x': (x',y)\in R, then y provides certain guarantees. So as long as the block looks like it plausibly follows the rule, we have some guaranteed properties of the outcome. For example, some users might be censored but for the users who are included we can provide some guarantees. Note, this is strictly better than the status quo.
Rules like these are particularly useful because we can stick them right into consensus (or enforce by smart contract in this case). Alternatively, an optimistic fraud-proving system could be used by any party who has access to a block to slash a misbehaving validator. Note that if r wasn’t in P, we couldn’t really be upset at a block builder for not enforcing it.
No, we do need the input to know if the block is valid according to r
An example of this is Penumbra’s planned’s transaction execution rule, which involves solving a convex optimisation problem over a given set of transactions and then rewarding each user according to the solution of this problem. Naturally, knowing that the numerical solution is correct requires knowing what the actual numbers in the input were.
Assuming we have reliable and publicly accessible knowledge of the input really opens the door to a lot of ordering rules - anything in P (and also some things functions, as I will explain later), but realising this assumption isn’t necessarily that easy. Some new mechanism must provide a reliable commitment to the input. However, if you know that some function is going to be applied to a certain input then you can toy with the input to find your desired output. Whoever is executing this new mechanism which commits to the input has incentive to deviate from simple truthful reporting (especially if they can see the input trickle in with time). Additionally, extra mechanisms could introduce other limitations like additional latency or hardware requirements.
Penumbra plans to deal with this problem by using a threshold decryption scheme which reveals nothing about the transactions until they have been committed to in a batch and a threshold of the validator set has signed off on the input.
An alternative way of dealing with this problem is through decentralisation. An example of this is Themis which gives its guarantees (FIFO ordering) based on an honest majority assumption, where we can think of the input as a set of tuples which consist of a transaction and its timestamp. Apart from ensuring an honest majority, you also need to find some way of ensuring that everyone participating agrees on the input. A second example is this proposal on the forum which would be a general input commitment device for many ordering rules.
Another way of dealing with this problem would be to treat the rule as not in P and use some of the possible solutions for these kinds of rules.
Q2.2: Given that r is not in P, is there a sufficient approximation rule for r?
In other words, is there some other rule which gives a result that’s close enough that I’m happy?
Yes, I have an approximation rule
We can go back to Q1 with the new rule. Examples of relaxations like these could be to at least exceeding some lower bound which is achievable in polynomial time or just plainly executing a different rule which isn’t that much worse than the original rule.
No, I don’t have an approximation rule
This is the status quo in Ethereum today. Validators want to impose the rule “maximise my coinbase payment,” but finding the ordering which does maximise this payment is known to be NP-hard. For rules like this, it seems like the best we can aim for want is for whoever is ordering the block to give a best effort in approximating this rule.
Two broad approaches (usually used in tandem):
-
incentivisation: If the agent is incentivised to execute a rule as well as possible, they will, with more incentive implying more effort. This is what happens in PBS. Clearly there is incentive to produce valuable blocks, but a competitive market has to be created to make sure that this value actually flows to the proposer. Although, one could imagine a different rule which does not need a market and a simple incentive would do.
CoWswap presents an interesting variation on such a competitive market, where the biggest deviation comes from the offer of an exogenous reward (i.e. CoWswap protocol pays solvers per batch) and the need to commit to input (currently done in a trusted manner). -
constraints: it may be desirable to implement some sub-rules to contstrain the space of outcomes such that the incentivisation has its desired effect. An example of this would be CoWswap constraining batches to clear at a uniform clearing price while asking for optimisation of a value called surplus. The uniform-clearing-price sub-rule prevents solvers from optimising surplus in a way that is undesirable according to CoWswap’s objectives.
Other considerations
-
Multiblock deviations. We have considered rules which apply on a per-block basis, but since multiple blocks are produced in reality, we could want rules that extent past a single block. E.g. the greedy sequencing rule does not provide guarantees against an adversary who controls two blocks in a row (who can stack all trades in one direction in one block and then arb at the top of the next).
-
The abstraction of transaction ordering rules has some obvious shortcomings. For example, in PBS the rule is hard to verify because the input to the problem differs between builders. The input differs because different agents have different views of the mempool (and maybe exclusive order flow), but also because builders start off with different utility functions and access to liquidity. Producing the most valuable block might require inserting additional transactions or being willing to pay more for the same thing than someone else (because builders value assets differently at any given point in time).
-
I haven’t mentioned cryptographic approaches much, but there’s certainly a large design space that leverages cryptographic rules to constrain block builders. An easy example is taking some algorithm which is hard to verify without the input, running it inside and SGX and relying on that for faithful execution. Of course, this will have different trust assumptions to other kinds of rules (but beats what L2s are doing now).
Please suggest rules or desiderata that I missed or roast what I already have. Rules with examples are particularly desirable.