TEEs can easily provide a “one shot signature” or “anti-equivocation” feature. This is very powerful and underrated, even in the projects otherwise pushing the limits with TEEs. Let’s make some clear illustrative examples that use this to its fullest.
The basic appeal is this: We should be able to place deposits to a key controlled by a TEE - now, any transactions signed by that TEE can be considered gauranteed-finalizable because of the non-equivocation. The TEE would be ensuring the key is only used in a write-once way, so if you’re holding a signature from the TEE you know it can’t be contradicted by any other signature. Such signatures could be passed around like instant-finality certificates, including from one TEE to another.
The challenge is we’ll still have to deal with Availability. The singular TEE controlling the active key could crash. We could run a consensus protocol among the TEEs but that would undermine the benefits of instant-finality-from-Non-equivocation.
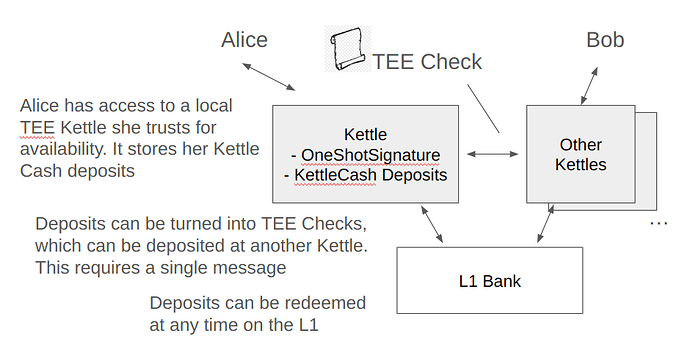
What we might try instead is something like a “federated” service. When your coins are deposited in a single Kettle, you will be subject to the risk of that Kettle becoming unavailable. However, the Kettle will be able to issue you a “claim check” which you can very easily deposit somewhere else. Here’s an illustration:
Here’s (a paper I like) from Sattath and Ben-David about constructing efficient e-cash using a “One Shot Signature.” They envision instantiating this using Quantum states, but we can just replace the word “quantum” everywhere with “TEE” instead and understand it as a suapp. Specifically section “8.1 Sending Quantum Money over a Classical Channel” gives an interesting story about using these one-shot signatures to make an e-check system.
[we show] a quantum money scheme that is derived from a tokenized (either private or public) signature scheme. In particular, we show how to convert a quantum bill into a classical “check”, which is addressed to a specific person and can be exchanged for a quantum bill at a bank branch. Recall … a testable public (private) digital signature scheme satisfies the definition of a public (resp. private) quantum money scheme, with the signing tokens acting as the quantum bills. Now, in this setting, if Alice holds a quantum bill, one thing she can do is spend it the usual way. However, an alternative thing she can do with the bill is use it to sign a message. Such a signature will necessarily consume the bill, and hence can be used as proof that Alice has burned her bill.
In particular, consider what happens if Alice signs the message, “I wish to give a bill to Bob”. Alice can send over this classical signature to Bob, who can verify the signature using the public verification scheme. Bob can then show this signature to his bank branch. Crucially, the bank knows that Alice burned her bill, since the signature is valid; hence the bank can safely issue Bob a bill. In essence, this
usage converts a quantum bill into a classical check!
I think the biggest remaining limitation of this proposal described her is the lack of recourse if a users’ preferred TEE crashes. It would be nice to have a backup option, if the quantum key gets stuck then the last holder can claim it on L1. I think this could be improved by adding a “Recovery key” and an associated timeout, but this got confusing to think about.
The main related work for using write-once payments using TEEs and blockchains is TEEChan and TEEChain / (github). Although these are defined in terms of channels, they seem to function a lot like the checks described here. They put some work into mitigating TEE compromise, whereas that’s explicitly left out of scope here.